Moral Dilemma Judgment

Hennig and Huetter (2020) proposed a multinomial model of moral dilemma judgment and evaluated the model in a series of experiments. Participants were presented with hypothetical scenarios that required a decision whether or not to break a moral norm.

Berentelg (2020) conducted a replication study that was designed to be similar to Experiment 2b in Hennig and Huetter (2020).

data(moraldilemma)

Format

MDHennig2020 A data frame consisting of seven variables:

selfrel

factor. Instructions about self-relevant consequences of the decision where either (absent) or (present).

congrcy

factor. Endorsement of consequences and norm endorsement lead to different decisions (incongruent) or to the same decision (congruent).

default

factor. The norm may be adhered to by continuing (inaction default state) or by changing (action default state) an ongoing behavior.

breaknorm

factor. Decision to break the norm.

exp1, exp2b

the aggregate response frequencies for Experiment 1 and 2b, respectively.

treeid

an identifier for the single trees of the joint multinomial model.

MDreplication A data frame containing 751 observations of five variables:

selfrel

factor. See above.

gender

factor. Participant gender.

age

participant age.

rt

median response time (in seconds) across scenarios.

y

a matrix of response frequencies per participant. Each column represents a combination of the factors congrcy, default, and breaknorm.

Source

Hennig, M., & Huetter, M. (2020). Revisiting the divide between deontology and utilitarianism in moral dilemma judgment: A multinomial modeling approach. Journal of Personality and Social Psychology 118(1), 22--56. doi: 10.1037/pspa0000173

Berentelg, M. (2020). Multinomial modeling of moral dilemma judgment: A replication study. Bachelor thesis. University of Tuebingen, Germany. https://osf.io/mb32t/

See also

mpt.

Examples

data(moraldilemma)

## Exp. 1: proCNI and process dissociation (PD) model
s <- mptspec("proCNI")
exp1 <- subset(MDHennig2020, selfrel == "absent")
mpt(update(s, .restr = list(J=I)),      data = exp1, freqvar = "exp1")
#> 
#> Multinomial processing tree (MPT) models
#> 
#> Parameter estimates:
#>      C       N       I  
#> 0.4215  0.5273  0.5601  
#> 
#> Goodness of fit (2 log likelihood ratio):
#> 	G2(1) = 1.183, p = 0.2768
#> 
mpt(update(s, .restr = list(I=0, J=1)), data = exp1, freqvar = "exp1")
#> 
#> Multinomial processing tree (MPT) models
#> 
#> Parameter estimates:
#>      C       N  
#> 0.4202  0.7615  
#> 
#> Goodness of fit (2 log likelihood ratio):
#> 	G2(2) = 1.814, p = 0.4038
#> 

## Exp. 2b: self-relevant consequences and norm endorsement
s <- mptspec("proCNI", .replicates = 2, .restr = list(J1=I1, J2=I2))
m1 <- mpt(s, data = MDHennig2020, freqvar = "exp2b")
m2 <- mpt(update(m1$spec, .restr = list(N1=N2)), data = m1$y)
anova(m2, m1)
#> Analysis of Deviance Table
#> 
#> Model 1: m2
#> Model 2: m1
#>   Resid. Df Resid. Dev Df Deviance Pr(>Chi)   
#> 1         3     8.7267                        
#> 2         2     0.5721  1   8.1546 0.004295 **
#> ---
#> Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

## Replication of Exp. 2b
md.agg <- aggregate(y ~ selfrel, MDreplication, sum)
y <- as.vector(t(md.agg[, -1]))

m3 <- mpt(s, data = y)
m4 <- mpt(update(s, .restr = list(N1=N2)), data = y)
anova(m4, m3)
#> Analysis of Deviance Table
#> 
#> Model 1: m4
#> Model 2: m3
#>   Resid. Df Resid. Dev Df Deviance Pr(>Chi)
#> 1         3     24.018                     
#> 2         2     21.671  1   2.3473   0.1255

coefs <- c(diff(coef(m3)[c("N2", "N1")]),
           diff(coef(m1)[c("N2", "N1")]))
names(coefs) <- c("Replication", "Hennig & Huetter\n(2020, Exp. 2b)")
ci <- coefs + rbind(
  qnorm(c(.025, .975))*sqrt(sum(diag(vcov(m3))[c("N2", "N1")])),
  qnorm(c(.025, .975))*sqrt(sum(diag(vcov(m1))[c("N2", "N1")]))
)
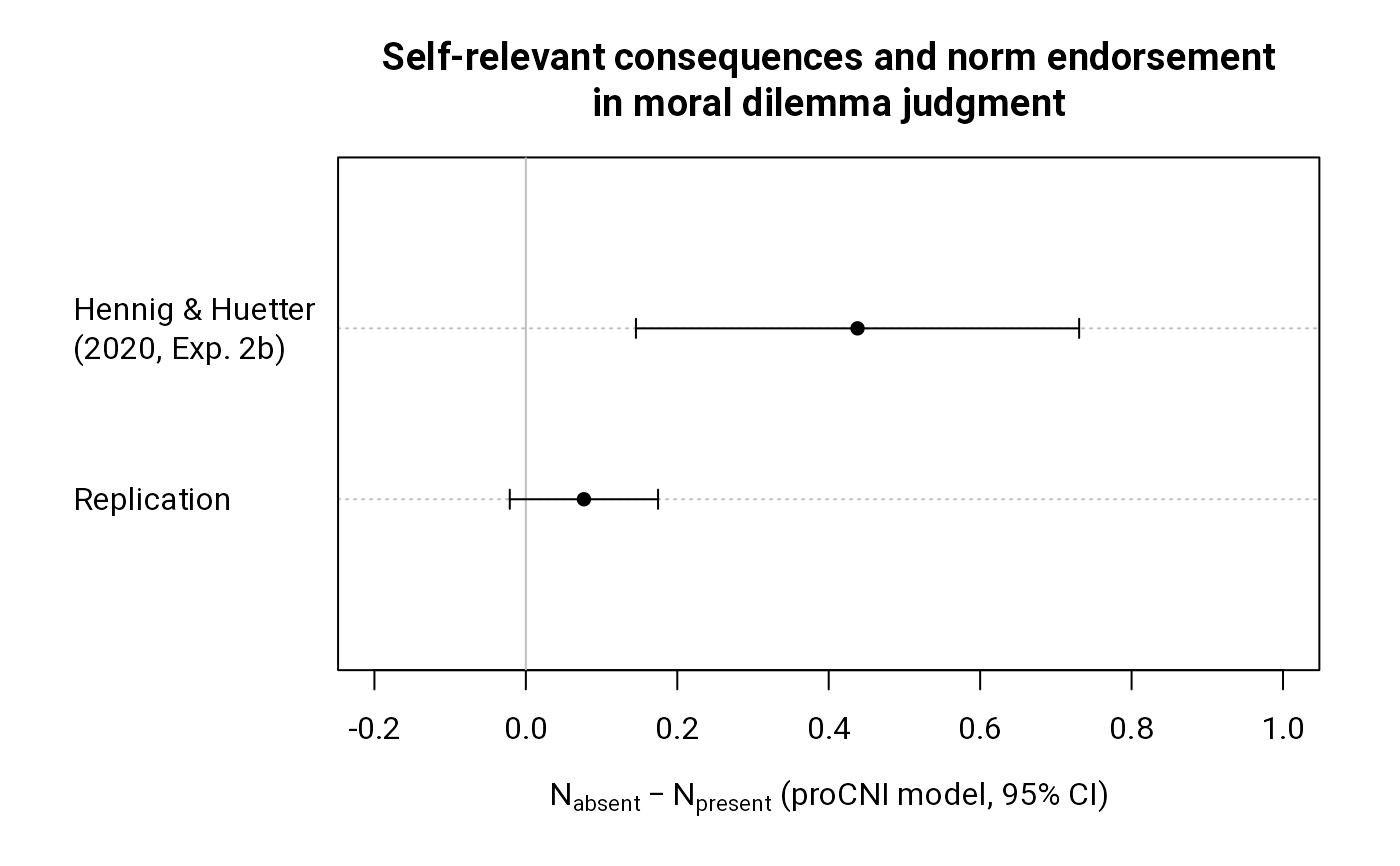
dotchart(coefs, pch = 16, xlim = c(-.2, 1),
  xlab = expression(N[absent] - N[present]~"(proCNI model, 95% CI)"),
  main = paste("Self-relevant consequences and norm endorsement",
               "in moral dilemma judgment", sep = "\n"))
abline(v = 0, col = "gray")
arrows(ci[, 1], 1:2, ci[, 2], 1:2, .05, 90, 3)