City-Size Paired-Comparison Task
citysize.RdIn a city-size paired-comparison task on each trial, participants judge which of two cities is more populous. After the paired comparisons, participants indicate for each city if they recognize its name. Hilbig, Erdfelder, and Pohl (2010) report a series of experiments to evaluate their model of recognition heuristic use at this task.
The WorldCities data are from a study designed to be similar to
Hilbig et al.'s Experiment 6. The 17 cities were (in order of population;
Wikipedia, 2016): Shanghai, Tianjin, Tokyo, Seoul, London, Bangkok,
Chongqing, Wuhan, Santiago, Rangun, Ankara, Harbin, Kano, Busan, Durban,
Ibadan, Montreal.
The ItalianCities data are from a study designed to be similar to
Hilbig et al.'s Experiment 7. The 14 cities were: Milan, Naples, Turin,
Palermo, Venice, Padua, Taranto, Prato, Reggio Emilia, Perugia, Cagliari,
Foggia, Salerno, Ferrara.
data(citysize)Format
WorldCities A data frame containing 37 observations of six
variables:
genderfactor. Participant gender.
ageparticipant age.
rtmedian response time (in seconds) across paired comparisons.
groupfactor. The control group (
CG) received standard instructions, the experimental group (EG) was instructed to choose the city they recognized whenever possible.countrynumber of cities whose country was correctly identified.
ya matrix of aggregate response frequencies per participant. The column names indicate each of eight response categories: correct/false responses when both cities were recognized (
KC,KF), when both were unrecognized (GC,GF), when only one was recognized and the recognized city was chosen (RC,RF), and when only one was recognized and the unrecognized city was chosen (UF,UC).
ItalianCities A data frame containing 64 observations of six
variables:
gender,age,rt,ysee above.
groupfactor. The control group (
CG) received standard instructions, the experimental group (EG) was asked to compare the cities with respect to their elevation above sea level.knowRHfactor. Does the participant have any knowledge about the recognition heuristic (RH)?
Source
The WorldCities data were collected at the Department of Psychology,
University of Tuebingen, in June/July 2016. The ItalianCities data
are from Rettich (2020). The original data are from Castela et al. (2014).
References
Hilbig, B.E., Erdfelder, E., & Pohl, R.F. (2010). One-reason decision-making unveiled: A measurement model of the recognition heuristic. Journal of Experimental Psychology: Learning, Memory, and Cognition, 36(1), 123–134. doi:10.1037/a0017518
Castela, M., Kellen, D., Erdfelder, E., & Hilbig, B.E. (2014). The impact of subjective recognition experiences on recognition heuristic use: A multinomial processing tree approach. Psychonomic Bulletin & Review, 21(5), 1131–1138. doi:10.3758/s13423-014-0587-4
Rettich, A. (2020). Application of the recognition heuristic: An experimental validation of the r-model. Bachelor thesis. University of Tuebingen, Germany. https://osf.io/mz47y/
Wikipedia. (2016). List of cities proper by population. Retrieved Jun 16 from https://en.wikipedia.org/wiki/List_of_cities_proper_by_population.
See also
mpt.
Examples
data(citysize)
## Fit r-model separately for each instruction type
mpt(mptspec("rmodel"), unname(WorldCities[WorldCities$group == "CG", "y"]))
#>
#> Multinomial processing tree (MPT) models
#>
#> Parameter estimates:
#> b g r a
#> 0.7410 0.5788 0.6018 0.7092
#>
#> Goodness of fit (2 log likelihood ratio):
#> G2(1) = 0.3846, p = 0.5351
#>
mpt(mptspec("rmodel"), unname(WorldCities[WorldCities$group == "EG", "y"]))
#>
#> Multinomial processing tree (MPT) models
#>
#> Parameter estimates:
#> b g r a
#> 0.7235 0.4294 0.8176 0.7049
#>
#> Goodness of fit (2 log likelihood ratio):
#> G2(1) = 0.004271, p = 0.9479
#>
## Test instruction effect on r parameter
city.agg <- aggregate(y ~ group, WorldCities, sum)
y <- as.vector(t(city.agg[, -1]))
m1 <- mpt(mptspec("rmodel", .replicates = 2), y)
m2 <- mpt(update(m1$spec, .restr = list(r2 = r1)), y)
anova(m2, m1) # more use of RH with recognition instruction
#> Analysis of Deviance Table
#>
#> Model 1: m2
#> Model 2: m1
#> Resid. Df Resid. Dev Df Deviance Pr(>Chi)
#> 1 3 49.463
#> 2 2 0.389 1 49.074 2.465e-12 ***
#> ---
#> Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
## Fit r-model separately for each task type
mpt(mptspec("rmodel"),
unname(ItalianCities[ItalianCities$group == "CG", "y"]))
#>
#> Multinomial processing tree (MPT) models
#>
#> Parameter estimates:
#> b g r a
#> 0.7660 0.4375 0.7469 0.8532
#>
#> Goodness of fit (2 log likelihood ratio):
#> G2(1) = 0.7389, p = 0.39
#>
mpt(mptspec("rmodel"),
unname(ItalianCities[ItalianCities$group == "EG", "y"]))
#>
#> Multinomial processing tree (MPT) models
#>
#> Parameter estimates:
#> b g r a
#> 6.399e-01 5.132e-01 2.050e-07 4.872e-01
#>
#> Goodness of fit (2 log likelihood ratio):
#> G2(1) = 23.03, p = 1.597e-06
#>
## Test task effect on r parameter
city.agg <- aggregate(y ~ group, ItalianCities, sum)
y <- as.vector(t(city.agg[, -1]))
m3 <- mpt(mptspec("rmodel", .replicates = 2), y)
m4 <- mpt(update(m1$spec, .restr = list(r2 = r1)), y)
anova(m4, m3) # less use of RH with elevation task
#> Analysis of Deviance Table
#>
#> Model 1: m4
#> Model 2: m3
#> Resid. Df Resid. Dev Df Deviance Pr(>Chi)
#> 1 3 446.12
#> 2 2 23.77 1 422.35 < 2.2e-16 ***
#> ---
#> Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
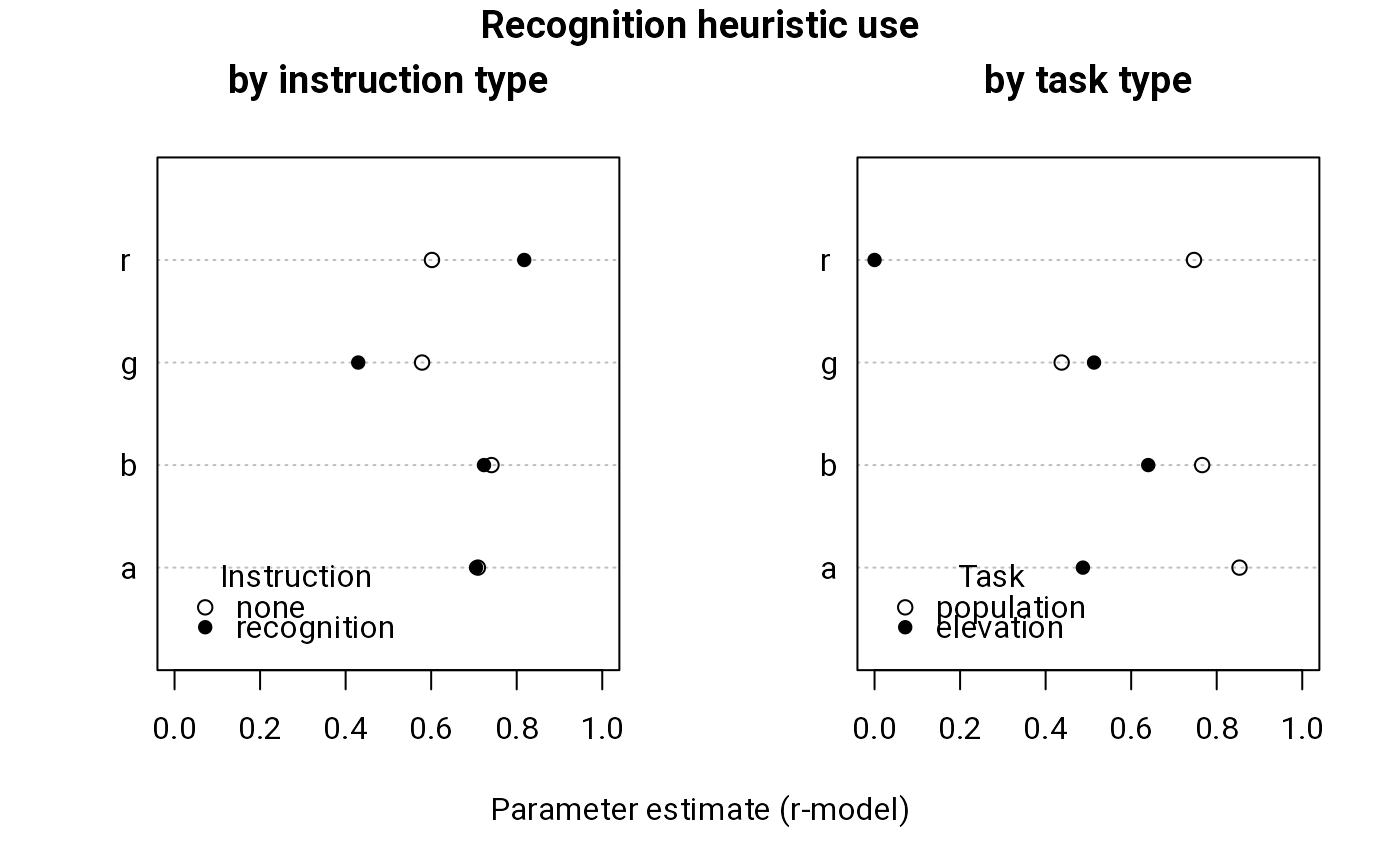
## Plot parameter estimates
par(mfrow = 1:2)
dotchart(coef(m1)[c(4, 1:3)], xlim = 0:1, labels = c("a", "b", "g", "r"),
xlab = "", main = "by instruction type")
points(coef(m1)[c(8, 5:7)], 1:4, pch = 16)
legend(0, 1, c("none", "recognition"), pch = c(1, 16),
title = "Instruction", bty = "n")
dotchart(coef(m3)[c(4, 1:3)], xlim = 0:1, labels = c("a", "b", "g", "r"),
xlab = "", main = "by task type")
points(coef(m3)[c(8, 5:7)], 1:4, pch = 16)
legend(0, 1, c("population", "elevation"), pch = c(1, 16),
title = "Task", bty = "n")
title("Recognition heuristic use", outer = TRUE, line = -1)
mtext("Parameter estimate (r-model)", side = 1, outer = TRUE, line = -2)
## Compare with original results
Hilbig2010 <- rbind(
WorldCities.CG = c(462, 204, 290, 272, 740, 205, 77, 62),
WorldCities.EG = c(500, 307, 279, 264, 902, 235, 68, 29),
ItalianCities.CG = c(232, 78, 135, 136, 465, 65, 56, 16),
ItalianCities.EG = c(245, 176, 154, 150, 228, 160, 112, 140)
)
apply(Hilbig2010, 1, mpt, spec = mptspec("rmodel"))
#> $WorldCities.CG
#>
#> Multinomial processing tree (MPT) models
#>
#> Parameter estimates:
#> b g r a
#> 0.6977 0.5160 0.6784 0.7537
#>
#> Goodness of fit (2 log likelihood ratio):
#> G2(1) = 0.2268, p = 0.6339
#>
#>
#> $WorldCities.EG
#>
#> Multinomial processing tree (MPT) models
#>
#> Parameter estimates:
#> b g r a
#> 0.6186 0.5138 0.8182 0.7861
#>
#> Goodness of fit (2 log likelihood ratio):
#> G2(1) = 0.03021, p = 0.862
#>
#>
#> $ItalianCities.CG
#>
#> Multinomial processing tree (MPT) models
#>
#> Parameter estimates:
#> b g r a
#> 0.7275 0.4982 0.6468 0.8654
#>
#> Goodness of fit (2 log likelihood ratio):
#> G2(1) = 3.011, p = 0.08271
#>
#>
#> $ItalianCities.EG
#>
#> Multinomial processing tree (MPT) models
#>
#> Parameter estimates:
#> b g r a
#> 0.5841 0.5066 0.2038 0.5313
#>
#> Goodness of fit (2 log likelihood ratio):
#> G2(1) = 0.01572, p = 0.9002
#>
#>